Harmonic analysis

   Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on unbounded domains such as the full real line or by Fourier series for functions on bounded domains, especially periodic functions on finite intervals. Generalizing these transforms to other domains is generally called Fourier analysis, although the term is sometimes used interchangeably with harmonic analysis. Harmonic analysis has become a vast subject with applications in areas as diverse as number theory, representation theory, signal processing, quantum mechanics, tidal analysis, spectral analysis, and neuroscience.

The term "harmonics" originated from the Ancient Greek word harmonikos, meaning "skilled in music". In physical eigenvalue problems, it began to mean waves whose frequencies are integer multiples of one another, as are the frequencies of the harmonics of music notes. Still, the term has been generalized beyond its original meaning.

One of the most modern branches of harmonic analysis, having its roots in the mid-20th century, is analysis on topological groups. The core motivating ideas are the various Fourier transforms, which can be generalized to a transform of functions defined on Hausdorff locally compact topological groups.

One of the major results in the theory of functions on abelian locally compact groups is called Pontryagin duality. Harmonic analysis studies the properties of that duality. Different generalization of Fourier transforms attempts to extend those features to different settings, for instance, first to the case of general abelian topological groups and second to the case of non-abelian Lie groups.

Harmonic analysis is closely related to the theory of unitary group representations for general non-abelian locally compact groups. For compact groups, the Peter–Weyl theorem explains how one may get harmonics by choosing one irreducible representation out of each equivalence class of representations. This choice of harmonics enjoys some of the valuable properties of the classical Fourier transform in terms of carrying convolutions to pointwise products or otherwise showing a certain understanding of the underlying group structure. See also: Non-commutative harmonic analysis.

If the group is neither abelian nor compact, no general satisfactory theory is currently known ("satisfactory" means at least as strong as the Plancherel theorem).

The 7 Coolest Mathematical Discoveries of 2024

 The 7 Coolest Mathematical Discoveries of 2024

Unsolvable problems, many-dimensional wheels and new prime numbers are among new mathematical discoveries this year.

Here’s a look at a few of the most exciting mathematical discoveries we wrote about this year.

NEW SHAPE DROPS

A mathematician wondered how few corners a shape could have and still fit together to completely cover a surface with no gaps. This quandary led him and his colleagues to discover shapes that had never been described mathematically before, called soft cells. Though they are new to mathematicians, it turns out that soft cells are found inside nautilus shells, red blood cells and other elements of nature.

SUPERLONG PRIME

Prime numbers—numbers divisible only by 1 and themselves—have long fascinated mathematicians. This year a researcher discovered the largest known prime number, with a whopping 41,024,320 digits. It had been six years since the last new prime number was discovered, and the search is getting harder and harder because prime numbers spread out farther from each other as they grow.

NEW RECIPE FOR PI

The concept of pi (π), the ratio of a circle’s circumference to its diameter, has been well known for 4,000 years, since ancient Babylonia. But calculating the exact digits of this irrational number has always been a challenge. Recently physicists used string theory to come up with an entirely new method for calculating pi.NEW RECIPE FOR PIThe concept of pi (π), the ratio of a circle’s circumference to its diameter, has been well known for 4,000 years, since ancient Babylonia. But calculating the exact digits of this irrational number has always been a challenge. Recently physicists used string theory to come up with an entirely new method for calculating pi.

A WHEEL IN MULTIPLE DIMENSIONS

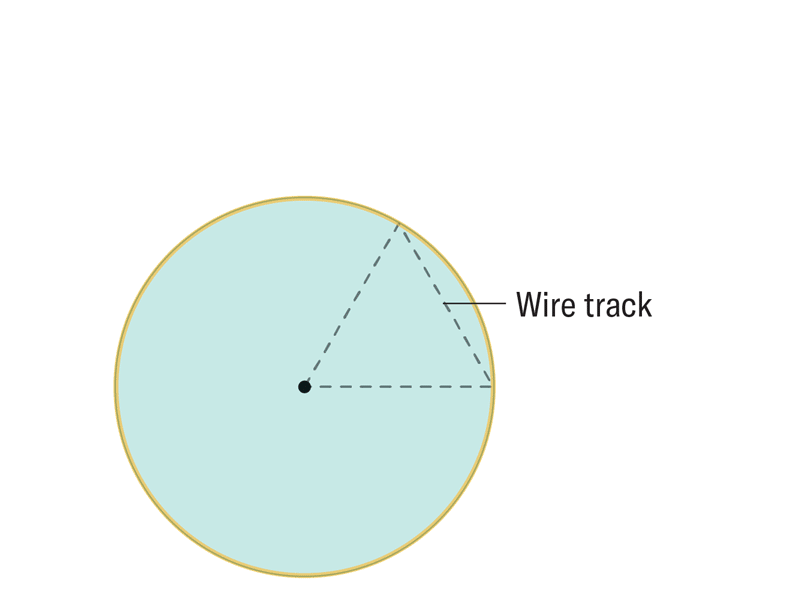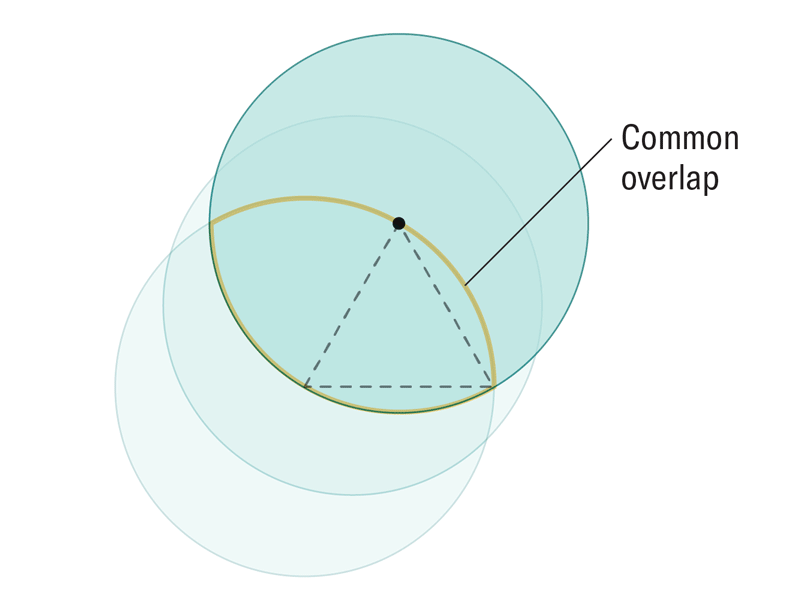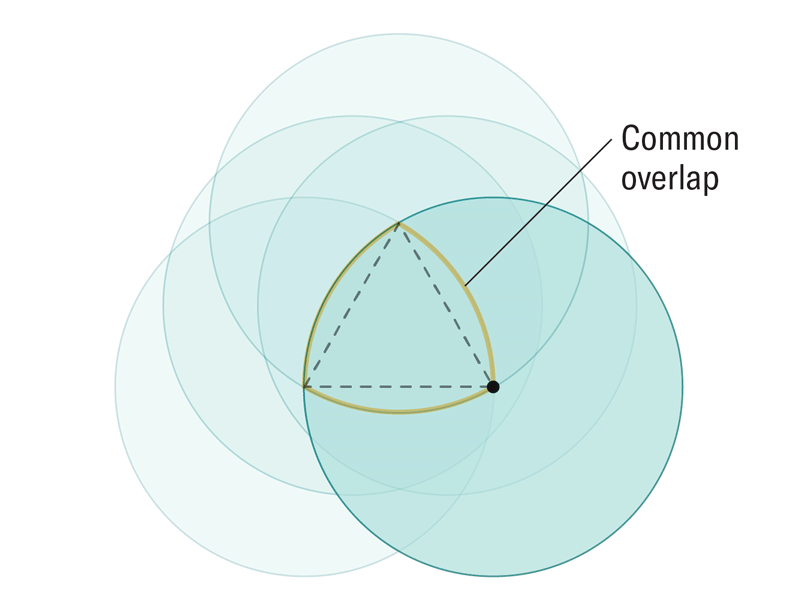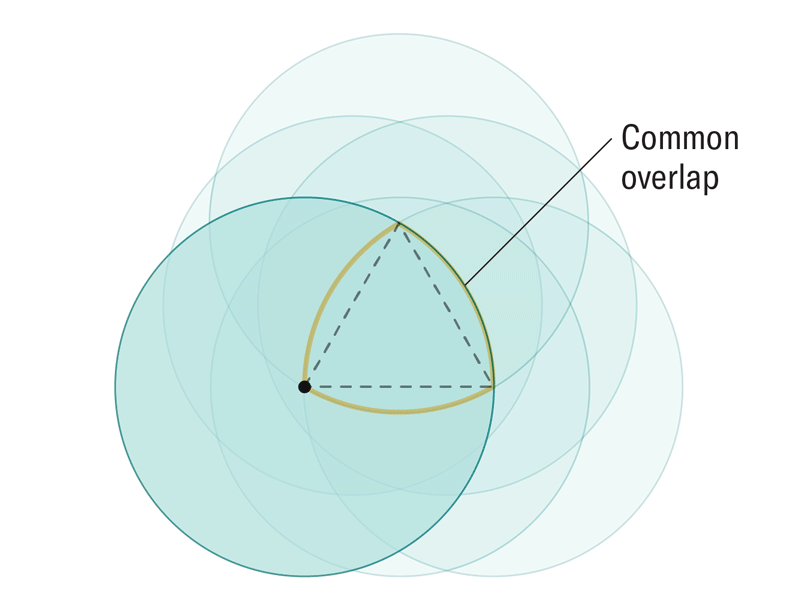
For 40 years, mathematicians have pondered a question: How can we find constant-width shapes with the minimum volume in any dimension? Researchers recently envisioned a new kind of many-dimensional wheel to answer this question. The newfangled wheels can be constructed in any dimension at a fraction of the size of more traditional rolling shapes, such as circles or spheres.

CALCULATING THE INCALCULABLE

This breakthrough has to do with a fundamental truth in mathematics: not everything can be calculated, no matter how hard one tries (or how busy of a beaver they are). A particular noncalculable expression is called the busy beaver function. Its values, called BB(n), will never be known for all quantities of n, but an international collaborative project called the Busy Beaver Challenge recently succeeded in determining the fifth value of the function—surprising mathematicians who thought it would be impossible.

J. S. BACH’S HIDDEN MESSAGES

Scientists turned musical scores written by Baroque composer Johann Sebastian Bach into mathematical networks and analyzed how his different styles varied. They used information theory to find patterns in his music that help explain how Bach conveyed messages—including musical, mathematical and emotional information—through his works.

THE MISSING TILE

Mathematicians had long wondered whether a single shape could ever tile a surface—that is, cover a plane completely—without creating a repeating pattern. Many doubted that such a shape, dubbed an einstein tile, could exist, but researchers finally discovered one. Though the tile was announced in 2023, one of the mathematicians involved gave us his behind-the-scenes account of the story this year.

R

International Conference on "Interdisciplinary Research on Mathematics & Statistics" ICIRMS-2024

 

Most and Least Lucrative Mathematics Occupations in U.S.

 

Mandelbrot set

                 

Mandelbrot set:

               The Mandelbrot set is a famous fractal that exhibits intricate and self-similar patterns at every level of magnification. It is defined by a simple iterative algorithm involving complex numbers. The set is named after the mathematician Benoît B. Mandelbrot, who studied and popularized it in 1980.

Definition:

The Mandelbrot set consists of all the complex numbers 

$c$

$$z_{n+1} = z_n^2 + c$$

does not escape to infinity when iterated starting with 

$z_0 = 0$$c$$z_n$$n$

Key Concepts:

• Complex Numbers: A complex number is of the form 
  $c = a + bi$$a$$b$

• Escape Time Algorithm: To check if a complex number belongs to the Mandelbrot set, we repeatedly square 
  $z_n$$c$$|z_n|$$z_n$

• Visualization: When visualizing the Mandelbrot set, points that are in the set are typically colored black, while points that escape are colored based on how fast they escape. This creates a beautiful and complex image that shows spirals, filaments, and other intricate shapes.

Steps to Generate a Mandelbrot Set Image:

1. Choose a region of the complex plane: Typically, you choose a rectangular area of the complex plane (e.g., real values between -2 and 2 and imaginary values between -1.5 and 1.5).
2. Iterate over each pixel: For each point in the grid, treat the 
   $x$$c$$y$
3. Apply the iterative formula: Start with 
   $z_0 = 0$$z_{n+1} = z_n^2 + c$
4. Check if the point escapes: If 
   $|z_n| > 2$
5. Plot the points: Points that remain bounded are part of the Mandelbrot set and are typically plotted in black. 
6. What does the Mandelbrot set represent?
7. 

   The Mandelbrot set is an example of a fractal in mathematics. It is named after Benoît Mandelbrot, a Polish-French-American mathematician. The Mandelbrot set is important for chaos theory. The edging of the set shows a self-similarity, which is perfect, but because of the minute detail, it looks like it evens out.

Properties of the Mandelbrot Set:

1. Self-Similarity: The set shows self-similarity at different scales. As you zoom into any part of the boundary, you continue to find structures similar to the whole set.

2. Fractal Nature: The Mandelbrot set is a fractal, meaning its boundary is infinitely complex and detailed. As you zoom in, you reveal more intricate patterns.

3. Connectedness: The Mandelbrot set is a connected set. This means that it is "one piece" and does not break into multiple disconnected parts.

4. Complex Boundary: The boundary of the Mandelbrot set is highly intricate, containing infinitely many filaments and intricate structures.

Applications and Uses:

• Mathematics and Chaos Theory: The Mandelbrot set is often used in mathematics to explore complex dynamics, nonlinear systems, and chaos theory.
• Art and Visualization: Its stunning visuals make it a favorite in artistic representations of mathematics and fractals.
• Computer Graphics: It serves as a standard example for algorithms in computer graphics and fractal rendering.

Would you like me to generate an image of the Mandelbrot set for you, or do you need more detailed explanations on specific aspects of it?

mathematical wonders of the world