Mathematical sciences:
Mathematical sciences is a group of areas of study that includes, in addition to mathematics,
those academic disciplines that are primarily mathematical in nature
Statistics,
for example, is mathematical in its methods but grew out of scientific observations which merged with inverse probability and grew through
applications in the social sciences,
some areas of physics and biometrics to become its own
separate, though closely allied field of mathematics. Computer science, computational science, population genetics, operation research, cryptology, econometrics, theoretical physics,
and actuarial science are other fields that
may be considered as part of mathematical sciences.
A long-standing practice has been to divide the
mathematical sciences into categories that are, by implication, close to
disjoint. Two of the most common distinctions are drawn between “pure” and
“applied” mathematics, and between “mathematics” and “statistics.” These and
other categories can be useful to convey real differences in style, culture and
methodology, but in the Panel’s view, they have produced an increasingly
negative effect when the mathematical sciences are considered in the overall
context of science and engineering, by stressing divisions rather than unifying
principles. Furthermore, such distinctions can create unnecessary barriers and
tensions within the mathematical sciences community by absorbing energy that
might be expended more productively. In fact, there are increasing overlaps and
beneficial interactions between different areas of the mathematical sciences.
Applied
mathematics
Applied mathematics is the application of mathematical methods by different fields such as science, engineering, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied
mathematics" also describes the professional specialty in which mathematicians work on practical problems by
formulating and studying mathematical models.
In the past, practical applications have motivated the
development of mathematical theories, which then became the subject of study in
pure mathematics where abstract concepts are studied for their own sake. The
activity of applied mathematics is thus connected with research in pure mathematics.
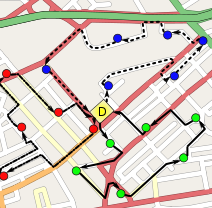
Efficient solutions to the vehicle routing problem require tools from combinatorial optimization and integer programming.
Historically, applied mathematics consisted of applied analysis, most notably differential equations; approximation theory (broadly construed, to include representations, asymptotic methods, variation methods, and numerical analysis); and applied probability.
These areas of mathematics related directly to the
development of Newtonian physics, and in fact, the
distinction between mathematicians and physicists was not sharply drawn before
the mid-19th century.
This history left a pedagogical legacy in the United States:
until the early 20th century, subjects such as classical mechanics were often taught in applied mathematics departments at
American universities rather than in physics departments,
and fluid mechanics may still be taught in applied mathematics departments.