3D Coordinate Geometry - Equation of a Plane
A plane is a flat, two-dimensional surface that extends infinitely far. A plane is the two-dimensional analog of a point (zero dimensions), a line (one dimension), and three-dimensional space. A plane in three-dimensional space has the equation
where at least one of the numbers and must be non-zero. A plane in 3D coordinate space is determined by a point and a vector that is perpendicular to the plane.
A plane in 3D coordinate space is determined by a point and a vector that is perpendicular to the plane. Let be the point given, and the orthogonal vector. Also, let be any point in the plane, and and the position vectors of points and respectively. Now, if we let then since is perpendicular to we have
We can also write the above equation of the plane as
where
This does not quite work if one of is zero.In that case the vector is parallel to one of the coordinate planes. Say then the vector is parallel to the -plane and the equation of the required plane is which is of course a straight line in the plane and is unrestricted. Similar arguments apply if two of are zero.
Another way to think of the equation of the plane is as a flattened parallelepiped. A flattened parallelepiped, made of three vectors , has volume 0. We can use the scalar triple product to compute this volume:
where gives the vector that is normal to the plane.
Let's say that the endpoints of are and and the components of are . Then by taking the dot product, we get the equation of a plane, which is
A plane is a flat, two-dimensional surface that extends infinitely far. A plane is the two-dimensional analog of a point (zero dimensions), a line (one dimension), and three-dimensional space. A plane in three-dimensional space has the equation
where at least one of the numbers and must be non-zero. A plane in 3D coordinate space is determined by a point and a vector that is perpendicular to the plane.
A plane in 3D coordinate space is determined by a point and a vector that is perpendicular to the plane. Let be the point given, and the orthogonal vector. Also, let be any point in the plane, and and the position vectors of points and respectively. Now, if we let then since is perpendicular to we have
We can also write the above equation of the plane as
where
This does not quite work if one of is zero.In that case the vector is parallel to one of the coordinate planes. Say then the vector is parallel to the -plane and the equation of the required plane is which is of course a straight line in the plane and is unrestricted. Similar arguments apply if two of are zero.
Another way to think of the equation of the plane is as a flattened parallelepiped. A flattened parallelepiped, made of three vectors , has volume 0. We can use the scalar triple product to compute this volume:
where gives the vector that is normal to the plane.
Let's say that the endpoints of are and and the components of are . Then by taking the dot product, we get the equation of a plane, which is
The equation of a plane which is parallel to each of the -, -, and -planes and going through a point is determined as follows:
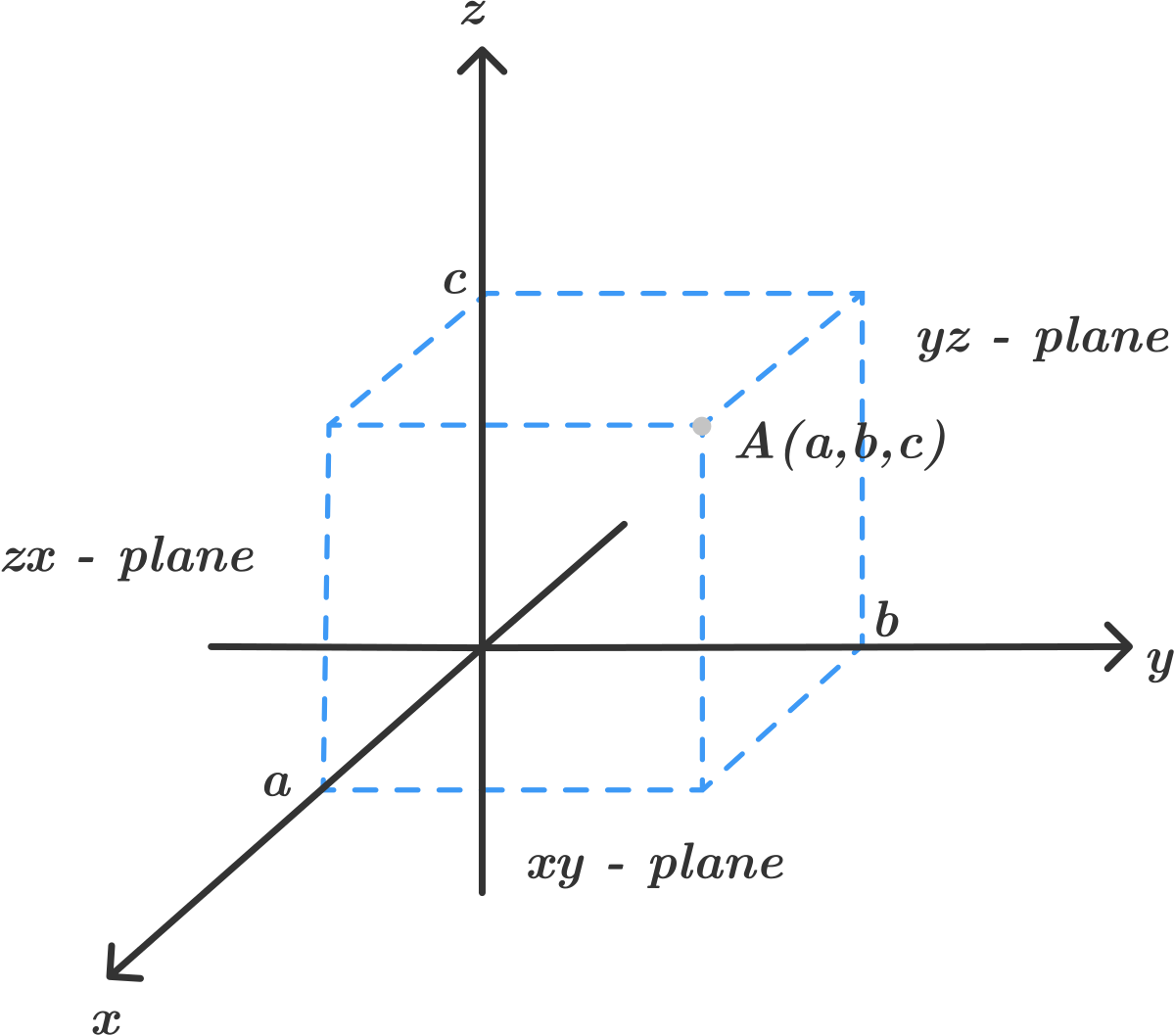1) The equation of the plane which is parallel to the -plane is
2) The equation of the plane which is parallel to the -plane is
3) The equation of the plane which is parallel to the -plane
The equation of a plane which is parallel to each of the -, -, and -planes and going through a point is determined as follows:
1) The equation of the plane which is parallel to the -plane is
2) The equation of the plane which is parallel to the -plane is
3) The equation of the plane which is parallel to the -plane
2) The equation of the plane which is parallel to the -plane is
3) The equation of the plane which is parallel to the -plane
Normal Vector and a Point
If we know the normal vector of a plane and a point passing through the plane, the equation of the plane is established.
Thus, the equation of a plane through a point whose normal vector is is
